1次元セル・オートマトン
ライフゲームをさらに簡素化したものが1次元セル・オートマトンである。2次元セル・オートマトンのモデルは簡素であるが考えられる組み合わせが余りに多すぎる。1次元セル・オートマトンではたかが256通りの組み合わせしかない。
1次元セル・オートマトンは自身と左右のセルの合計3つのセルによって決定される。3つのセルの取りうる組み合わせは8パターンあり、その結果として返るセルは白か黒の2通り、つまり28=256通りである。2次元セル・オートマトンでは全世代を一度に表示するには3次元の図が必要であった。しかし1次元セル・オートマトンでは全ての世代を重ね合わせた図は2次元になる。つまり1世代目からn世代目までを一目で見渡すことができる。
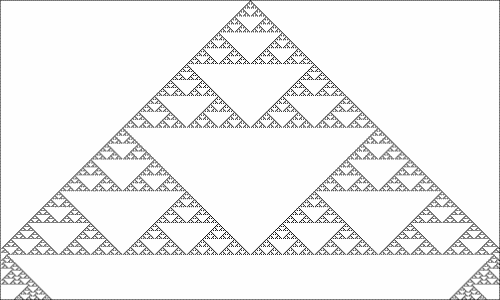
以下はJavaScriptによる1次元セル・オートマトンである。1〜256の規則番号によって描画される結果が大きく異なってくる。また初期世代を1点固定にすることができる。例えば規則番号90番で一点固定をチェックして描画すると美しいフラクタル図形が描かれる。
(2008/08/02)近傍2マスまで広げクラス4の複雑性を実行できるタイプのデモを公開。
クラス
256パターンある1次元セル・オートマトンを調べたスティーブン・ウォルフラムはこれを4つのクラスに分類した。
クラス1

有限の世代内に真っ黒若しくは真っ白に収束するタイプ。
クラス2

若い世代はバラバラでも世代を重ねると安定した模様に落ち着くタイプ。
クラス3

白と黒がバラバラに出現するタイプ。ほぼランダムなカオス状態。
クラス4

3つのクラスにも分類できない。安定状態に収束せず、またカオス状態ともいえないタイプ。自然の複雑系はこのクラス4から成り立っていると考えられている。
※256パターン内にもこれに近い振る舞いをするものがあるが、クラス4は近傍2マスまで範囲を広げないと得られないとされる。