概要
2007/09/09
過去2回続いたJavaScriptで連立方程式を計算する試み第3弾。
第1弾は単なる4次までの展開公式、第2弾は展開公式をその場で計算しているものの、コードが全く最適化されていなかった。今回の計算プログラムは行列計算ライブラリを用いており、若干の改良余地(※1)があるものの計算量自体は最適化されている。具体的に各次数での計算サイズを表にすると以下のようになる。第3弾の計算サイズであるn!は行列式の計算に要する計算量としては最小限となっている。
| n |
第2弾(nn) |
第3弾(n!) |
無駄な計算量 |
計算効率 |
| 2 |
4 |
2 |
2 |
50.00% |
| 3 |
27 |
6 |
21 |
22.22% |
| 4 |
256 |
24 |
232 |
9.38% |
| 5 |
3125 |
120 |
3005 |
3.84% |
| 6 |
46656 |
720 |
45936 |
1.54% |
| 7 |
823543 |
5040 |
818503 |
0.61% |
| 8 |
16777216 |
40320 |
16736896 |
0.24% |
| 9 |
387420489 |
362880 |
387057609 |
0.094% |
| 10 |
10000000000 |
3628800 |
9996371200 |
0.036% |
| 11 |
285311670611 |
39916800 |
285271753811 |
0.014% |
前回第2弾で20分以上かけて計算した7次は、第2弾の計算量にして82万。これの半分の計算量で今回の第3弾の計算プログラムは9次(計算量36万)まで計算できることになる。ただし、36万個の巨大配列をスムーズに作成できれば、の話だが。
尚、8次以降の"解の公式"のテキストデータは、どう考えてもサイズが巨大すぎるため今回は載せない。
計算方法
2007/09/16
単純に連立方程式を行列で表し、逆行列を掛けることによって解を求めている。ちなみに第2弾ではクラメル公式を利用していた。
例えば、2元1次連立方程式。
- a11x+a12y=b1
- a21x+a22y=b2
これを行列で表すと次のようになる。
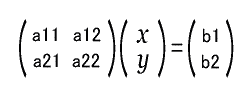
行列Aの逆行列(インバース)をA-1とすると、解(x,y)は次のように求められる。

n元の行列に一般化した場合、最初の式をAX=BとするとX=A-1Bで計算できる。これを実現するには利用している行列ライブラリにおいて次のように記述するだけで良い。
//A,Bを行列オブジェクトとする。
X = Matrix.Mul(A.Inverse(),B);
計算フォーム
2007/09/09
第2弾ではフォーム生成時に解の式を算出する方式だったが、今回はライブラリの都合上計算処理開始後に解の式を計算する。したがって、別に次数を増やせば11元のフォームも現れるが、計算ボタンを押した後に4000万個(しかも2次配列なので、実際には4000万*11)の配列を作ろうとするので、間違いなくメモリ不足で計算が強制終了される。もちろんその辺は警告以前にロックされているので、このフォームから計算できるのは8元1次連立方程式までとなっている(9元1次連立方程式は1時間経っても計算が終わらないため、今時点では安全を考慮して8元まで)。
初期値にはフォーム生成時に自動生成したサンプルの連立方程式が代入されている。値が確定できない方程式は不親切ながら「計算不能」を吐くのみとなる。尚、全て小数での計算になるので、整数解であっても計算途中の誤差で無限小数になることがある(1.99999999等)。そのため、小数点の桁数を制限する機能も与えられている。
手元のマシン(ブラウザはIE6)で、各次数での所要時間。行列ライブラリの特性上、同じ次数の行列の逆行列は2度目以降はキャッシュを用いて高速化されている。
8次1回目の総合計時間は(手元の環境と方式では)タイマーが正常に作動せず計測不能だったが、大体10分程度で計算できるはず。2回目以降では、8元1次連立方程式が現実的な時間で計算できる。キャッシュの効果は大きな連立方程式になればなるほど有効になってくる。
9元は試した限りでは1時間以上を要すると思われるが、前述のように安全を考慮して今の時点では計算できなくしてある。計算が出来る確認が取れれば、警告付きで追加したい。
(2007/09/16)プログラムの処理が重複していた問題を解消。2回目の処理1回分に相当する時間を削減できた。タイマーが正常に作動しない問題は、関数の最後にalert();を入れると直ることが判明。計算終了後に所要時間と終了時の時間を表示させて、タイマーの問題を解決。
計算時間
| n |
1回目 |
2回目以降 |
| 2 |
0ms |
0ms |
| 3 |
0ms |
0ms |
| 4 |
0-15ms |
0-15ms |
| 5 |
30ms |
15ms |
| 6 |
250ms |
50ms |
| 7 |
5500ms |
500ms |
| 8 |
340000ms |
5000ms |