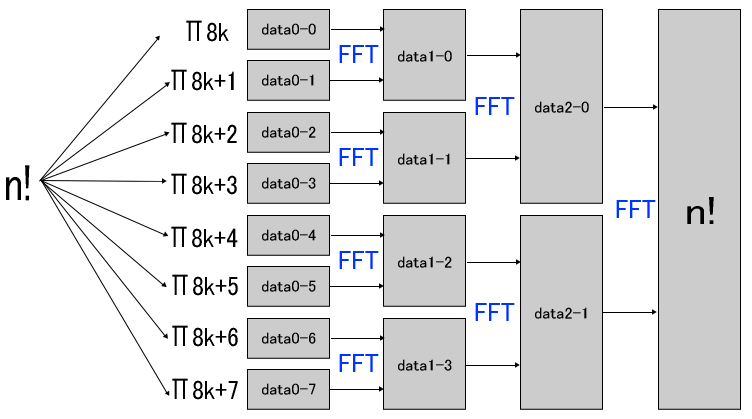
JavaScriptによるFFT乗算
2011/01/18-17:20
随分昔から、理想的にはこれで計算したいよね、と言っていたFFTを使った乗算プログラムを実際に作った。未調整で拙い出来だが、このコードで既に従来より速い。試験的にこれをHugeInt Ver.0.5 alpha6に乗せてみたものの変数の格納形式が大きく違い、そのまま使うと無駄が多いことが判明した。継ぎ接ぎ挿入ではお話にならないので、新しくVer.0.6系として基盤部分の再構築を考える。
12月は欠番となり久しく日記が飛んでいる。最近作ったデータの処理が追いついていない。近いうちにどうにかしたいところだが・・・。
試験実装のためHugeInt用に書き直したコード。
HugeInt.mulFFT = function( n1,n2 )
{
var Number1 = HugeInt.airi( n1.Copy() );
var Number2 = HugeInt.airi( n2.Copy() );
var Result = new HugeInt(0,false);
var al = HugeInt.__array;
var i,j;
var n1 = new Array();
var n2 = new Array();
var len1 = Number1.Val.length;
var len2 = Number2.Val.length;
for(i=0; i<len1; i++)n1[i] = [i,Number1.Val[i],0];
for(i=0; i<len2; i++)n2[i] = [i,Number2.Val[i],0];
var len1 = n1.length;
var len2 = n2.length;
if(len1>len2)for(i=len2; i<len1-len2; i++)n2[i] = [i,0,0];
else for(i=len1; i<len2-len1; i++)n1[i] = [i,0,0];
var len1 = n1.length;
for(i=len1; i<2*len1; i++)
{
n1[i] = [i,0,0];
n2[i] = [i,0,0];
}
n1_ft = HugeInt.fft(n1,-1);
n2_ft = HugeInt.fft(n2,-1);
n3_ft = new Array();
for(i=0; i<n1_ft.length; i++)
{
n3_ft[i] = new Array();
n3_ft[i][0] = n1_ft[i][0];
n3_ft[i][1] = n1_ft[i][1]*n2_ft[i][1]-n1_ft[i][2]*n2_ft[i][2];
n3_ft[i][2] = n1_ft[i][1]*n2_ft[i][2]+n1_ft[i][2]*n2_ft[i][1];
}
n3 = HugeInt.fft(n3_ft,1);
Result.Val = String();
var tmp = 0;
var padding_INT = HugeInt.INT[al];
for(i=0; i<n3.length; i++)
{
n3[i][1] = Math.abs(n3[i][1])+tmp;
Result.Val = HugeInt.padding[al](Math.round(n3[i][1]%padding_INT)) + Result.Val;
tmp = Math.floor(n3[i][1]/padding_INT);
}
Result.CutZero();
Result.flag = ( Number1.flag == Number2.flag ) ? false : true;
return Result;
}
HugeInt.fft = function( n1,flag )
{
var Result = n1;
var m = 2;
var n = 1;
var i;
while( m<Result.length )
{
m *= 2;
n++;
}
for(i=Result.length; i<m; i++)Result[i] = [i,0,0];
ResultX = HugeInt.dft(Result,m,n,flag);
return ResultX;
}
HugeInt.dft = function(d,m,n,f)
{
var i,j,k;
var revbit = function( b,n )
{
var c = 1;
var d = 0;
for(var i=0; i<n; i++)
{
d += c*((b>>(n-i-1))%2);
c *= 2;
}
return d;
}
// bit reverse & sort
for(i=0; i<m; i++)d[i][0] = revbit( i,n );
d.sort(HugeInt_fft_bitsort);
//butterfly
var pr,pi,qr,qi,m2,m3,omegar,omegai,theta;
theta = f*2*Math.PI;
m2 = 1;
for(i=0; i<n; i++)
{
theta *= 0.5;
m3 = m2*2;
for(j=0; j<m2; j++)
{
omegar = Math.cos(theta*j);
omegai = Math.sin(theta*j);
for(k=j; k<m; k+=m3)
{
pr = d[k][1];
pi = d[k][2];
qr = d[k+m2][1];
qi = d[k+m2][2];
d[k][1] = pr+omegar*qr - omegai*qi;
d[k][2] = pi+omegar*qi + omegai*qr;
d[k+m2][1] = pr-omegar*qr + omegai*qi;
d[k+m2][2] = pi-omegar*qi - omegai*qr;
}
}
m2 = m3;
}
if(f==1)for(i=0; i<m; i++)
{
d[i][1] /= m;
d[i][2] /= m;
}
return d
}
function HugeInt_fft_bitsort(a,b){return a[0]-b[0]}