HugeFloat Ver.0.6 開発日記
2014/06/28
HugeFloat Library>HugeFloat Ver.0.6
JavaScriptによる多倍長演算ライブラリの開発ノート。
以下、HugeFloat Ver.0.6の開発記録。
基本構成はVer.0.5を引き継ぎ、FFTと浮動小数点を追加する。
作ったプログラムのバージョン一覧。
歴代の演算能力(GoogleChromeを使用)
| 処理内容 |
Int Ver.0.3 |
Int Ver.0.4 |
Int Ver.0.5 |
Float Ver.0.6 a1 |
Int Ver.0.6 a3 |
Int Ver.0.6 a7 |
| 2の10000乗 |
140ms |
40ms |
40ms |
40ms |
20ms |
10ms |
| 2の100000乗 |
10000ms |
1300ms |
1000ms |
200ms |
100ms |
30ms |
| 2の1000000乗 |
-- |
-- |
不能(500000 over) |
7000ms |
1000ms |
160ms |
| 1000の階乗 |
130ms |
40ms |
40ms |
40ms |
40ms |
20ms |
| 10000の階乗 |
16000ms |
2200ms |
2200ms |
300ms |
300ms |
85ms |
| 100000の階乗 |
-- |
-- |
不能(2000000 over) |
8900ms |
8900ms |
4000ms |
| 10000桁÷10桁 |
300ms |
15ms |
15ms |
15ms |
100ms |
10ms |
| 10000桁÷100桁 |
470ms |
60ms |
60ms |
100ms |
100ms |
70ms |
| 10000桁÷1000桁 |
1300ms |
250ms |
250ms |
350ms |
100ms |
70ms |
| 100000桁÷10000桁 |
不能 |
20000ms |
20000ms |
27000ms |
2100ms |
900ms |
| 1000000桁÷100000桁 |
-- |
-- |
-- |
不能 |
57000ms |
19000ms |
2014年06月28日
FFT除算において精度の限界から商がずれる問題を内部的に10桁分の余剰精度を持たせることで解決。この問題は割る数と割られる数が近い時に起きる。
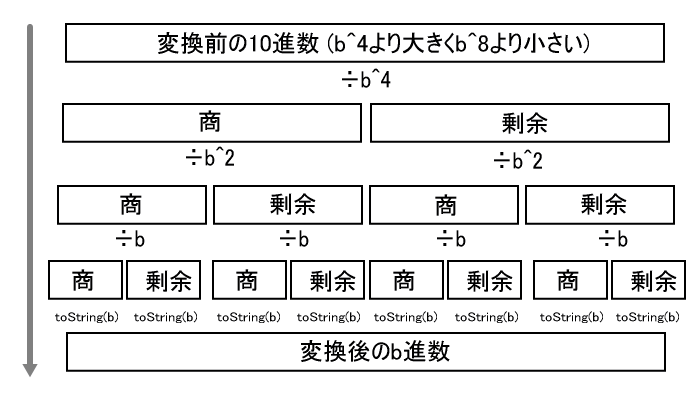
b進数へ変換するtoString関数を大幅に高速化。これまでは変換する数をb進数の基数で繰り返し割り続けて剰余を得ていたが、新たな方法では二分割法を用いて高速化した。変換する数をD、基底をbとするとき、D>b^2^nとなる最大のnを求め、Dをb^2^nで除算した商と剰余を配列に格納する。今度は各配列に対してb^2^(n-i)で除算して同じことを繰り返す。つまり、Dをb^2^n進数に変換し、それらをb^2^(n-1)進数に変換する操作を繰り返して最終的にb^2^0進数を得る。除算の回数そのものは同じものの、割られる数と割る数の桁数の差が2倍以下になるため、大きな桁数ではFFT除算を使えるようになる。またb^2^nは既存の累乗アルゴリズムを用いて瞬時に計算できる。toString関数は5000桁オーダーで速度10倍となった。
新しいtoString関数を逆向きで行うことで16進数から10進数への再変換も高速化。こちらは除算よりも軽量な乗算だけを使うためより速い。
以下は模式図。実際に使う基数bはJavaScriptの有効精度内で最大のb^kを選んでいる。b^k進数に変換した数列を最終的にJavaScriptのネイティブのtoString(b)で変換しても同じになるからだ。
2014年05月28日
FFT除算の軽微なバグ修正と16進数から10進数への再変換を実装。
素数検索にミラーラビン法を追加。
2012年02月21日
凍結されていた浮動小数点への対応を開始。alpha8でHugeFloatオブジェクトの導入、alpha9で加減算に対応、alpha10で乗算に対応した。
HugeFloatオブジェクトはHugeIntオブジェクト全体を覆う形で拡張されるようになっている。HugeInt単体でも動作し、Float用のファイル群を追加することで浮動小数点に対応する。逆に、Float用のファイルを読み込んでも従来通りIntも使用できるようになっている。どうしても余分な処理が増える上に有効精度が決まっているFloatより、Intを使いたい場面も想定している。
Floatの読み込みにともなって一部のHugeIntオブジェクトはFloatを扱えるように上書きされるが、基本的には別のものなのでIntでFloatを扱うことはできない。逆にFloatでIntを扱うことはできる。Floatオブジェクトで追加された要素は浮動小数点と有効精度の2つで、残りのパラメータはIntをそのまま使用している。
HugeIntでは入力されるデータ形式はどんなものでもよく、自動的に符号と数字以外を消去して読みこむようになっているが、HugeFloatではDDD.DDDe±DDDの浮動小数点形式の読み込みが可能になった代わりに、数字以外の記号が混ざると浮動小数点として読み込むことができなくなる(判別に正規表現を使っているため)。
2011年05月18日
speed.jsが完成し、FFT除算の実装に成功。100万桁÷10万桁の除算が1分→20秒に短縮された。
新しい方法による平方根の計算も実装したものの、現時点では遅い。これを解決するに、精度をわざと悪くして計算する乗算関数を作りたい。現状、n桁×n桁の上位n桁が欲しい場合2n桁の乗算を実行してから下位n桁を捨てている。しかし例えば大文字を上位n桁、小文字を上位n桁として分割した状態で乗算を行うと、(A+a)*(B+b)=AB+aB+bA+abが得られ、ab項はn桁程度しかないので無視できる。一方aBとbAは3n/2桁あり、捨てるのは下位n/2桁で済むようになる。
2011年03月29日
加算のバグ修正、除算の仕様の修正に伴い、除算を使った各関数を修正。大きな変更点はなく、依然としてspeed.jsによる速度計測ルーチンの研究中。
2011年03月08日
FFTを修正。speed.jsを搭載しての速度測定試験より、FFT関数はJavaScriptの組み込み関数を使うより直接式を記述したほうが速く、2次元配列よりも1次元配列で済ませるほうが遥かに高速になることが判明した。よって通常のRealDFTは1次元配列を使用したものとし、乗算時の2数同時FFTも廃止した。5万桁×5万桁のFFT乗算速度はGoogleChrome上でalpha4の3倍、1万桁÷1千桁のFFT除算速度は同2倍。
更新分がたまってのアップデートであるので未調整、動作は全く保障しないので注意。
2011年02月13日
FFT除算とLegacy(通常)除算の両方を個別に高速化。FFT除算では最後に実行する被除数と除数の逆数を乗算する処理は商と同じ精度があれば十分に計算できる。よって除数側の精度に加え被除数の精度も商程度に制限して乗算の桁数を削減した。
Legacy除算も同様の考えで高速化。n桁÷m桁の除算は大体n-m桁程度の商となるが、n-m<mならば、除数の精度をn-mに、被除数の精度を2(n-m)にしても商は変わらない。すなわち、除数の桁数が被除数の半分の桁数より大きいとき、計算する最大の桁数は商の2倍で固定されるようになった。
また剰余は次のようにして求める。上記の条件で高速化のためにカットする下桁数は2m-n桁である。被除数の上位桁部分をA、カットする下位桁をa、除数も同様にBとbとする。A÷Bの商X,剰余Yの関係はA=BX+Yである。一方桁数をカットしないときの商X剰余yとの関係は、A+a=(B+b)X+yである。従ってこの2つの方程式より、y=a+Y-bXで求められる。Yの下2m-n桁はゼロであり、aは2m-n桁なのでa+Yは計算しなくても良い。
2011年02月08日
オブジェクト名を一度HugeIntに戻した。当初の予定ではHugeIntは全面的にHugeFloatに置き換えるつもりであったが、HugeFloat上でIntを使うとFloat型に要する全ての処理がくっついてきてしまう。そこでHugeIntの速度を落とさないためにもInt単体で作成し、HugeFloatはHugeIntの関数群を他所から利用する方式とする。よって主要な関数群が揃うまでInt型を使う。
通常(レガシー)乗算とFFT乗算の自動切り替えを搭載。当初は掛け合わせる両方の数が1000桁未満のときにレガシー乗算を使うように設計されていたが、mul.jsを読み込む際に1280桁(2^8×5)の乗算を繰り返し実行し、レガシー乗算とFFT乗算の計算時間が等しくなる1280桁×X桁のXを探すようにする。Firefox環境で1280桁の2の乗数倍についても同様の計算を実行した結果、5*2^p桁の計算時間が等しくなる桁数はおおよそX/8*p*log10(p)であることを突き止めた。ただしこれはFirefoxのみであって、GoogleChromeでは再現できなかった。しかしそれほど大きな差ではない。読み込み時にXを計算し、以後それ以上の桁数については近似式を使ってレガシー乗算とFFT乗算を切り替えるようにした。これによって乗算関数HugeInt.mulはLegacyとFFTの切り替えに対応した。
逆数法を使った除算を追加。B/AをB*(1/A)とするような(1/A)をNewton法とFFT乗算を用いて計算する。1万桁以下では大きな差はないものの、10万桁クラスの除算はこれまでの除算では時間がかかりすぎるが、この新しい除算なら現実的な時間内で計算できる。10万桁÷1万桁が30秒から2秒に短縮(GC)、更に100万桁÷10万桁を1分で計算できた。乗算のような分岐コードはまだ搭載していない。また、同様の計算方式を平方根に対しても実装する予定。
2011年01月21日
オブジェクト名をHugeFloatに変更、浮動小数点を扱えるように各部を修正したが、まだ演算には一切反映していない。
基本オブジェクトの変更点は、既存のデータ格納形式,Array型とString型に加え、新たにFFT型を追加した。変換関数はHugeFloat.fuko()とした。ただし、FFTを主体とした乗算を行うために、Array型の桁数は7桁から5桁に落とされており、FFT型とArray型の区別はまだついていない。
FFT乗算によって、乗算・累乗・階乗が圧倒的に高速化された。その速度は桁数の多い領域でVer.0.5の10倍〜100倍以上であり、計算時間よりも先にブラウザのキャパシティーに収まりきらなくなるほど速い。メモリーを多く積んでいないコンピュータで計算すると、数十万桁規模の計算は途中で停止する可能性がある。
alpha1で2の100万乗がFirefox3.6上で10秒を切り、alpha2で1秒台になった。ver.0.5では2の100万乗は100秒程度かかっていた。階乗計算は前Ver.0.5の自己ベスト60000!(1228秒)を5.5秒で完了させる。事実上、10万の階乗や2の100万乗規模の計算が手に収まるほどのものとなった。
詳しい計算方法は日記でまとめ、まとまり次第ページに追加していく予定。
素数計算と円周率計算のページは一旦消去、この2つの速度は以前と変わっていない。今後デモページに統合して復活させる予定。
2011年01月19日
FFT乗算の試験の続き。FFT乗算を利用したFFT階乗を搭載。
2011年01月18日
Ver.0.5にfftパッケージ、fft.jsを搭載したFFT乗算の試験。
HugeFloat Ver.0.6
- 2014年06月28日
- alpha12
- 2014年05月28日
- alpha11
- 2012年02月21日
- alpha8
- alpha9
- alpha10
- 2011年05月18日
- alpha7
- 2011年03月29日
- alpha6
- 2011年03月08日
- alpha5
- 2011年02月13日
- alpha4
- 2011年02月08日
- alpha3
- 2011年01月21日
- alpha1
- alpha2
- 2011年01月19日
- 05alpha7b-2
- 05alpha7b-3
- 2011年01月18日
- 05alpha7b
