これは何?
シマウマの縞模様はどのようにしてできるのか、チーターの斑点はどのようにしてできるのか、考えたことはないだろうか。
まあ、あまり考える機会もないと思う。ではこの機会に考えてみよう。
たとえば司令塔になるような細胞がいて縞の一本一本、斑点の一個一個の形成を制御しているのだろうか。そんなことができるのか?体表の一個一個の細胞に的確に指示を与えることができるのか?
それとも特定の司令塔はいなくて、体表の細胞同士の相互作用で模様が形成されるだろうか。相互作用だけで規則立った模様を形成できるのか?
チューリングモデルはこの疑問に対する答えのひとつだ。チューリングモデルは後者の考え、つまり細胞同士の相互作用によって縞模様や斑点といった模様を形成できることを示すモデルだ。詳しい内容は後で述べる。
このアプリケーションではチューリングモデルをセルオートマトンによってシミュレートすることで縞模様や斑点、さらにはもっと複雑な模様を再現する。
試してみる
Canvas要素を使用。WebWorkerに対応しているブラウザを使うことをお勧めします(対応してなくても動くけどブラウザの動作が重くなるはず)。
チューリングモデルとは
アラン・チューリング、といえば情報系の人ならチューリングマシンを思い浮かべると思うが、この人は晩年生物学にも取り組んでいる。
1952年にチューリングが発表した論文では先に述べた体表の模様のような生体のパターン形成を2つの物質の細胞間での反応と拡散によって説明できるとした。それがこれから述べるチューリングモデルだ。
個々の細胞には活性化した状態と不活性な状態の2種類があるとしよう。活性化した細胞は2種類の物質を分泌する。活性化物質と阻害物質だ。活性化物質と阻害物質とではそれぞれ分泌する濃度や拡散する速度が異なる。
個々の細胞はまわりにある細胞から分泌された活性化物質と阻害物質の濃度によって状態が変わる。活性化物質が多ければ細胞は活性化し、阻害物質が多ければ不活性化する。
生体のパターン形成はこの作用だけで説明でき、パターンの違いは活性化物質と阻害物質の濃度や拡散速度で決まるというのがチューリングモデルの概要だ。(実際のモデルは微分方程式で説明されているが、ゆとりの僕にできる説明はここまでだ・・・。)
たとえば阻害物質よりも活性化物質の方が濃度も拡散速度も上回っていれば、1個だけ活性化した細胞がある状態からどんどん周囲の細胞が活性化され、その細胞も活性化物質を分泌することで最終的にすべての細胞が活性化される。
斑点のような模様は活性化物質よりも阻害物質の方が拡散しやすく、そのかわり活性化物質の方が濃い場合に現れる。縞模様はそれぞれの物質に拡散しやすい方向と拡散しにくい方向がある場合に発生する。
チューリングモデルはあくまで理論上のものと思われるかもしれないが、1990年にチューリングモデルを化学的に再現した実験において斑点模様の生成に成功しており、実際の生物の中で起きている仕組みとして十分考えられるだろう。
セルオートマトンによるチューリングモデルの再現
先にも述べたが、チューリングモデルそのものは微分方程式で与えられたモデルでその方程式自体を計算機上で数値的に解いてシミュレートする試みもあったが、相互作用によって表現するモデルであればもっと計算機に向いた別のアプローチがある。セルオートマトンだ。
セルオートマトンはセルが敷き詰められた空間で、個々のセルについて周囲のセルとの相互作用から次の時点でのセルの状態を求めていくことで現象をシミュレートする手法だ。セルオートマトンの代表例としてはConwayのライフゲームが知られている。
微分方程式で与えられたチューリングモデルは連続的なモデルだが、セルオートマトンは離散的なモデルであり、チューリングモデルをセルオートマトンによって再現するにあたってはうまい具合に離散化してやる必要が出てくる。
先の斑点模様の場合であれば、活性化物質は狭い範囲に濃く拡散し、阻害物質は広い範囲に薄く拡散する。この性質に基づいて単純化したモデルを今回採用した。
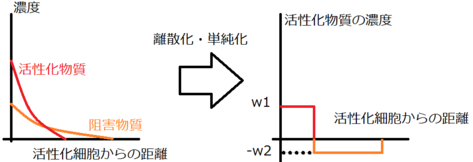
個々のセルが1つの活性セルから受ける作用は活性セルから対象のセルまでの距離から上図のグラフより求まる。作用は活性化物質の濃度により表され、正は活性化物質の作用、負は阻害物質の作用を表す。次の時点での個々のセルの状態は周囲の活性セルの作用の和によって定まり、正であればそのセルは活性化し、負であれば不活性化する。
等方性について
実際に上記のモデルでセルオートマトンを構成するにあたってセルの形状(正方形、正三角形、正六角形など)を選択することになるが、こうして構成されたオートマトンが導く結果がセルの形状に左右されないように気をつけなければならない。
セルの形状として正方形を選ぶとしよう。次の時点でのセルの状態を求めるにあたってそのセル(Aとしよう)と活性セル(同じくBとしよう)との距離を求める必要が出てくる。問題はAのどの点とBのどの点との距離を求めるかだ。
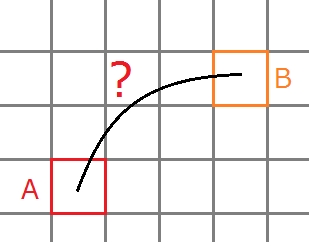
単純にA,Bそれぞれのセルの中央の点同士の距離を求めればいいと思うかもしれない。だが、これではだめなのだ。

上図は中央に1個だけ活性セルがある状態からシミュレートして得られた結果だ。セル間の距離としてセルの中央の点同士を距離を求めている。この結果は左右上下について対象であり、活性セルはおおよそ菱形に広がっていっている。この結果はセルの形状(この場合は正方形)の影響を受けているといえる。
このようなセルの形状による影響を回避するには、各セル内のランダムに選んだ点(代表点と呼ぶ)同士の距離をセル間の距離として求めればよい。
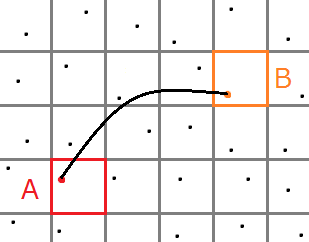
このセル間距離を採用して、中央に1個だけ活性セルがある状態からシミュレートした結果を下図に示す。非対称でセルの形状に影響されてないことが分かる。

実装について
通常のセルオートマトンの場合は隣接するセル同士でのみ相互作用が発生するが、今回のチューリングモデルの場合、ある一定距離内にある活性セルすべてと相互作用するため、1個のセルの状態更新で調べる必要のあるセルが多くなる。そのためセルの数に対して計算量が線形オーダであるとはいっても、セルオートマトンの状態更新は重い処理となる。
重い処理であれば当然長い時間他の処理をブロックすることになる。『他の処理』にはユーザのクリックに対するブラウザの反応なども含まれる。つまりユーザの動作に対するブラウザの反応が遅くなってしまうのだ。
この状況を避けるために今回の実装ではできるだけWebWorkerを使ってセルオートマトンに対する処理を別スレッドに投げている。通常のウェブページのスレッドからセルオートマトンの処理を切り離すことで通常のウェブページでの処理のブロックを回避しているのである。
とはいえどのブラウザもWebWorkerに対応しているわけではない以上、WebWorkerに対応してないブラウザでも(すごく動作が重くなるとしても)動くように配慮する必要があるだろう。ということでセルオートマトンスレッドと通常のウェブページスレッドとの通信の間にプロキシ的なオブジェクトを挟んでおき、WebWorkerに対応してるブラウザの場合はセルオートマトンスレッドと通信し、WebWorkerに対応していない場合はウェブページスレッド側でセルオートマトンの処理をするようにした(プロキシパターンですね)。
参考文献
- 『セルオートマトン法―複雑系の自己組織化と超並列処理』森北出版
- 今回のアプリケーションを作るきっかけになった書籍。Amazon
- David A. Young『A local Activator-Inhibitor Model of Vertebrate Skin Patterns』math. Biosci., 72,51-58 (1984)
- セルオートマトンによるチューリングモデルの再現に関する論文。SciVerse
- H.E. Schepers, M. Markus 『Two types of performance of an isotropic celluar automaton:stationary(Turing) patterns and spiral waves』Physica A,188,337-343(1992)
- セルオートマトンにおける等方性の問題の解決とそれに基づくチューリングモデルの再現に関する論文。SciVerse