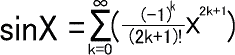π=lim[θ⇒0](180/θ)sinθを導く
2005/06/24
高校1年で習うレベルの数学を用いて円周率を計算することにする。ただし表記に極限を用いているが、極限の高度な式変形は一切用いない。この部分は後に分かるので、この式を1から求めてみよう。
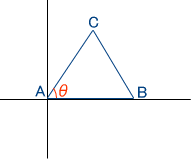
まずこのような三角形があったとする。 分かっている辺はACとAB。角はθが判明している。
小学校で習った三角形の面積公式は、面積=底辺×高さ÷2だった。 この三角形の面積を求めるには高さが足りない。 そこで、頂点CからABに対し垂直な線を引く。ABとの交点をHとする。
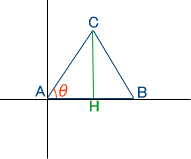
CHが分かれば面積が分かる。
CHはsinθ=CH/AC
CH=AC・sinθ
故に、三角形の面積は AB×AC×sinθ÷2となることが分かる。 この式を次の場合に適用する。
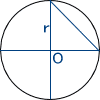
円の内部に三角形を描いた。 この三角形の2辺の長さは両方r。 その間の角の大きさは90゜である。
先の公式より、面積はr×r×sin90゜÷2 = r2sin90゜/2 = r2/2 。
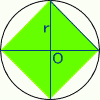
これより緑の部分の面積は 4(r2/2)となる。
この緑の部分の面積がどうしたんだということだが、角θの値を小さくしていってみよう。
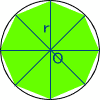
θが360/8、45゜の場合はこうだ。 どんどん緑の部分が円に近くなっていることが分かる。 これを無限に繰り返す。 これより多角形の面積は、(360/θ)r2sinθ/2
円の面積の公式はπr2。
(360/θ)r2sinθ/2で、θを0に近づけていったときの面積は円に近づく。
よって、(360/θ)r2sinθ/2 = πr2
式を整理し、(180/θ)sinθ = π (θは限りなく0に近い)となる。
この、θを0に近づける処理をlim[θ⇒0](180/θ)sinθと書く。即ち、
π=lim[θ⇒0](180/θ)sinθ