今のコンピュータは、内部では2進数を用いて様々な計算を行っている。 2進数とは、0と1だけで構成される数。
人間が普段使っているのは10進数、これは0,1,2,3,4,5,6,7,8,9までくると桁上がりし、10になる。
これに対し、2進数は0,1で桁上がりし10になる。 対応表は以下の通り。
10進数と2進数の対応表
| 10進数 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
… |
| 2進数 |
0 |
1 |
10 |
11 |
100 |
101 |
110 |
111 |
1000 |
… |
このように2進数は急激に桁数が増大する。 10進数を2進数に変換するスクリプトも組んだ。
何故コンピュータは2進数を使って演算しているのかといえば、2進数の0と1はコンピュータを流れる電流の有無に置き換えられるからだ。もちろん10進数でも計算できるが、例えば0を0V,1を0.5V,2を1Vに対応させた場合、ノイズなどで一時的に電流が小さくなった場合計算ミスが生じてしまう。また2進数だと掛け算も10進数の90種類に対し4種類しか存在しないため、掛け算の回路の設計は4種類の入力に対する出力を決定するだけで済む。そして10進数より桁数の多い2進数の計算量は現在のコンピュータの演算速度を以ってすれば全く問題にならない(とはいっても流石に1bitずつちまちまやると時間が掛かるため、今のコンピュータは32bitずつまとめて処理している)。
さて、2進数を使っていることは分かったが、具体的にどのようにしてこれを処理しているか。コンピュータでは2進数(電流のONとOFF)によって特定の処理を行う回路を論理ゲートと呼んでいる。実は大基となる論理ゲートはたった数種類しかない。
論理ゲート
全てのゲートを列挙する。 電流がONの場合をH(High)、OFFの場合をL(Low)とする。真理表とは、入力に対し出力がどう反応するかを示す。
ANDゲート(基本ゲート)
入力電流2つが共にHの場合だけ出力XがHになる。
ブール代数
X=A・B
ゲート記号

真理表
真理表
| A |
B |
X |
| L |
L |
L |
| L |
H |
L |
| H |
L |
L |
| H |
H |
H |
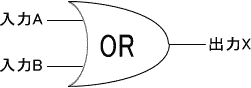
ORゲート(基本ゲート)
入力2つのうち少なくとも1つがHの場合、出力XがHになる。
ブール代数
X=A+B
ゲート記号
真理表
真理表
| A |
B |
X |
| L |
L |
L |
| L |
H |
H |
| H |
L |
H |
| H |
H |
H |
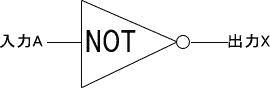
NOTゲート(基本ゲート)
入力した電流がHのときL、LのときHになる反転作用。
ブール代数
X=A
ゲート記号
真理表
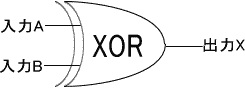
EX.ORゲート(XOR)
入力2つの値が等しい場合はL、等しくない場合Hを出力。排他的論理和と呼ばれ、基本ゲートのAND、NOT、ORを使って組み立てることができる。
ブール代数
X=A⊕B
AND、OR、NOTに分解したときの数式は
X= (A・B)+(A・B)
ゲート記号
真理表
真理表
| A |
B |
X |
| L |
L |
L |
| L |
H |
H |
| H |
L |
H |
| H |
H |
L |
NANDゲート
ANDゲートと全く逆の働きをする。NANDゲートだけで基本ゲートであるAND,OR,NOTを実現できる論理の完全性を持つ。
ブール代数
X=A・B
ゲート記号

真理表
真理表
| A |
B |
X |
| L |
L |
H |
| L |
H |
H |
| H |
L |
H |
| H |
H |
L |
NORゲート
ORゲートと全く逆の働きをする。NANDゲートと同じく論理の完全性を持つ。
ブール代数
X=A+B
ゲート記号
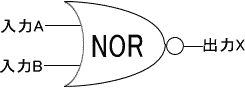
真理表
真理表
| A |
B |
X |
| L |
L |
H |
| L |
H |
L |
| H |
L |
L |
| H |
H |
L |
論理ゲートを再現
今までのは面倒だが一応説明しておかねばという前菜で、これが本命。 各ゲートの数式を組み合わせてデジタル回路(ブール代数)を構成し、それの数式を実際に動かすスクリプトを製造した。これによって、コンピュータ内部で行われている最も基本的な演算を擬似的に再現できる。
なお、使用可能な変数は大文字半角のA,B,C,D,E,Fの6種類。 26種類でもよかったのだが、処理が増えるのと、真理表を自動生成する機能のためだ。数式がインプットされると、まずその数式の全変数にLを代入し一度検算する。これでエラーを検出する。
四則演算回路
2006/05/20
コンピュータは基本となる論理ゲートを組み合わせて演算を行っている。そこで実際に1桁の四則演算を行う回路を組んでみる。1桁の2進数は入力パターンがたったの4種類しかないので、4種類の入力に対して正確な出力さえできる回路を組めば良い。
しかも先に紹介した論理ゲートで2つの入力に対する出力のパターンは全て網羅されているため、先の論理ゲートの知識があれば四則演算を実行するデジタル回路ぐらいは直ぐに分かる。
加算回路
2進数における加算は4種類。
- 0+0 = 00
- 0+1 = 01
- 1+0 = 01
- 1+1 = 10
真理表は次のようになる。AとBが入力、CとDが出力。Cが1桁目、Dが2桁目。
真理表
| A |
B |
C |
D |
| L |
L |
L |
L |
| L |
H |
H |
L |
| H |
L |
H |
L |
| H |
H |
L |
H |
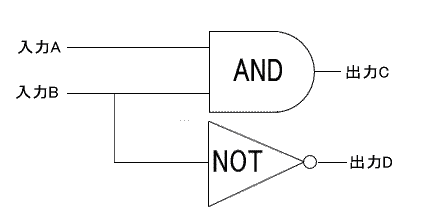
真理表を見れば分かるように、1桁目のCはAとBが共に違う値だったときにHになる。DはAとBが共にHだった場合だけHになる。つまり、CはAとBの排他的論理和—EX.ORゲート(XOR)1本で、DはAとBをANDゲートに通すだけでいい。
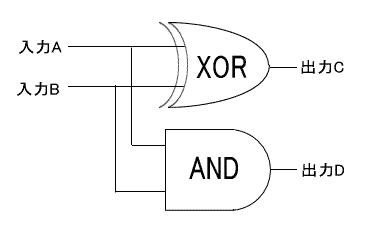
減算回路
2進数における減算は4種類。減算では桁上げはないが、答えが負になったときに桁下げ出力が必要になる。
- 0-0 = 0
- 0-1 = 1
- 1-0 = 1
- 1-1 = 0
真理表は次のようになる。AとBが入力、CとDが出力。Cが演算結果、Dは結果が負になった時だけHになる。
真理表
| A |
B |
C |
D |
| L |
L |
L |
L |
| L |
H |
H |
H |
| H |
L |
H |
L |
| H |
H |
L |
L |
Cの出力は加算と同じくEX.ORゲート(XOR)で実現される。Dの出力はAがL、BがHのときだけHにする必要がある。これにはAだけにNOTゲートを通した後ANDゲートを通せばよい。
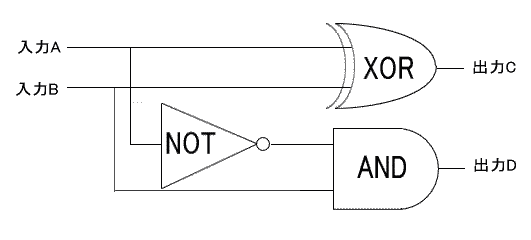
乗算回路
2進数における乗算は4種類。
- 0*0 = 0
- 0*1 = 0
- 1*0 = 0
- 1*1 = 1
真理表は次のようになる。AとBが入力、Cが出力。
真理表
| A |
B |
C |
| L |
L |
L |
| L |
H |
L |
| H |
L |
L |
| H |
H |
H |
真理表はANDゲートそのもの。ANDゲート1本で実現できる。
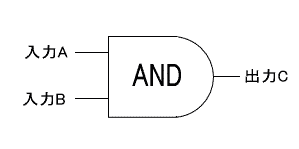
除算回路
2進数における除算は4種類。うち2種類は計算できない。なお実際の除算は1桁でやるようなものではないが、ここでは最小限の回路ということで1桁除算とする。
- 0/0 = 不確定(計算不可)
- 0/1 = 0
- 1/0 = 無限大(計算不可)
- 1/1 = 1
真理表は次のようになる。AとBが入力、Cが出力。Dはエラーを返す。
真理表
| A |
B |
C |
D |
| L |
L |
L |
H |
| L |
H |
L |
L |
| H |
L |
L |
H |
| H |
H |
H |
L |
Cは乗算と全く同じ。BがLのときは計算不能のためDをHにする、つまりBにNOTゲートを通すだけ。