近光速船による恒星間旅行の所要時間

概要

2009/03/19-2009/03/23

地球上で出せる光速より十分小さい速度(時速0km〜1000km)では、静止した物体もそれに対して動いている物体も、時計の針が進む速度は同じであり、相対速度は単なる加減算で表される。しかし、光速に近い速度(秒速300000km付近)では、特殊相対性理論によれば静止した物体に対して動いている物体に流れる時間の長さが変わり、相対速度は光速を超えられない。従って、この速度では同じ加速力を維持しても実際の加速はどんどん鈍ってしまう。地球に最も近い恒星でさえ、その距離は4光年以上離れており、人類の生み出した現在最速の人工衛星(ボイジャー1号,17km/s)でさえ、8万年もの時間がかかってしまう。

現実的な時間内(100年以内)に到達する場合、どうしても光速に近い速度での宇宙航行が求められ、前述のように低速ではありえなかった現象が生じてくる。この速度領域で長距離を航行する場合に、時間の流れの変化と加速率の変化を計算に入れると、具体的にどのような時間になっていくるのかを計算するツールを作成。

計算式

2009/03/19

相対論効果が無視できない場合の速度や時間を求めてみる。c=299792458[m]と定義し、光速度を1とした単位系を考える。

先ず、静止した系(地球など)における時間(客観時間)をt[s]とし、宇宙船における時間(主観時間)をτ[s]と定義する。速度v[c/s]で移動する宇宙船が、a[c/s²]の加速で微少時間dτ[s]内での速度の変化量は、a・dτ[c/s]になる。ニュートン力学ではdτ後の速度はv+a・dτで表されるが、vが光速に近い場合、特殊相対性理論の速度合成公式を用いなければいけない。

その式は

であり、変形すると

dτ→0とすると、左辺はv(τ)の微分の定義式となり

変数を揃えて両辺を積分すると

となる。この関数のグラフは

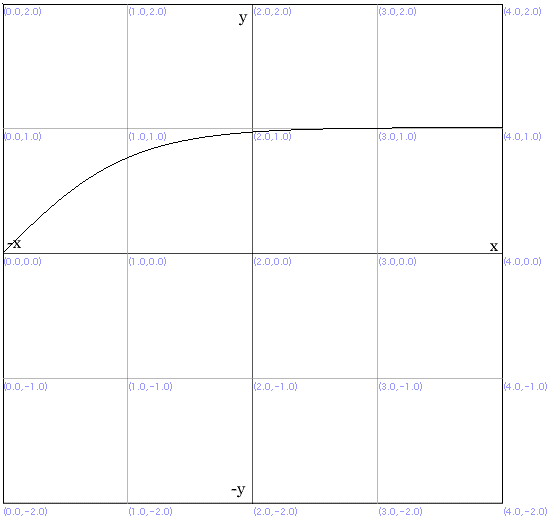
Graview ver.3.0.1において(Math.exp(x)-Math.exp(-x))/(Math.exp(x)+Math.exp(-x))を適用。

のような形となり、いくら等加速度運動を続けても速度は光速に漸近し続けるだけであることがわかる。

次に、外部時間tとの関係を求める。

dtとdτには

のような関係がある。v(τ)を代入すると

これを積分すると

が得られる。

sinhxのグラフは

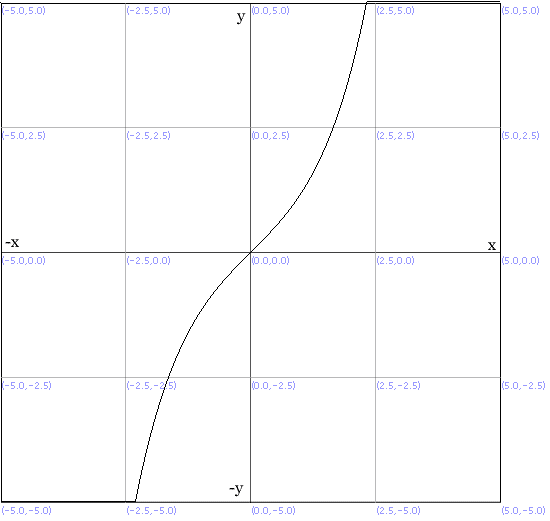
Graview ver.3.0.1において(Math.exp(x)-Math.exp(-x))/2を適用。

のようになり、光速に近づくにつれ宇宙船と外部の時間比は指数関数的に開いていくことがわかる。

宇宙船が進む距離xは

で求められ、先のdtとdτの変換式を用いて計算すると

これは宇宙船内の時間τに準じたものだが、tとτの変換式は導出済みである。

以上の結果を利用して、ある性能の宇宙船で恒星間旅行を行った場合、どの程度の時間がかかるのか計算してみよう。

計算ツール

2009/03/19

宇宙船の加速力を地球重力(G)換算で入力し、目標地点(LY)に到達するまでに必要な時間を計算する。ついでに、宇宙船の最高速度時に遭遇する宇宙塵の破壊力も計算できるようにした。

宇宙空間を移動する物体にとっては、加速と減速は原理的に同じことであるため、目的地点を目指す場合、目的地で丁度速度を0にしている必要がある。そのため、例えば10光年先に行くのに、光速に漸近する速度で10年しかかからないわけではなく、現実には加速時間と減速時間が必要になる。今回算出される数字は加速時間と減速時間を考慮したものになる。尚、初期値の4.37光年は最も近い恒星系であるαケンタウリまでの距離である。

入力

加速力

G

最大速度

C km/s

目的地までの距離

光年

※宇宙塵の質量g

出力

所要主観時間

所要客観時間

航行中に出した最高速度

C

全工程の内訳(船内)

加速区間: --

巡航区間: --

減速区間: --

宇宙塵のエネルギー

kJ

Debug

　

補足

2009/03/19

相対論的運動エネルギーの換算には次の式を利用した。質量m[kg]、光速度c=299792458[m/s](cの次元は速度)。ここでの速度v[c/s](cの次元は距離)は、光速を1とした値である。

あとがき

2009/03/19

発端としては地球に似た惑星が多数存在か、太陽から30光年以内に　国際ニュース : AFPBB Newsて記事(タイトルだけで決めたようなものだから、記事の引用は行わない)から、加速力を特定した上で近傍外宇宙へ乗り出す場合の感覚を計算したかった。2009年3月13日の日記にて計算した速度と所要時間の簡易スクリプトで言及されていた相対論効果について取扱うことも理由の1つに挙がる。この記事のスクリプトも部分的に利用している。

1G加速を持続できる宇宙船を主に想定しており、この1G加速を無限に持続できるなら主観時間で18年もあれば1万光年の彼方へ向かえてしまうことが分かる。しかし現実に計算されている宇宙船、例えば核融合推進では最大速度が0.1C程度だったりと、障害が多い。反物質エンジンなら加速力の上限は解消されるが、やはり燃料の問題が生じる。反物質エンジン利用時の積載燃料の計算も行いたかったが、これ以上機能を増やして特定させるのもいかがかと思ったため、反物質燃料の途方もない数字を見て現実を実感するのは次回とし、今回は星間物質との衝突の途方もないエネルギーを見て現実を実感するのみとした。

数式のMathML版はXHTMLデータを参照。

参考

2009/03/19

• 特殊相対性理論 - Wikipedia
• エネルギーの比較 - Wikipedia
• 静止エネルギー - Wikipedia
• 定加速航法のロケット力学（特殊相対性理論）